solicodes.blogg.se - Solve the formula of hanoi towers

Therefore, the time taken by an algorithm for Towers of Hanoi will be proportional to the number of times we move some disk. In our case, an elementary move is to move a disk from one rod to another rod. We know that the time taken by an algorithm will be proportional to the number of elementary moves made. If i % 3 = 0, make the legal move between rods and. If i % 3 = 2, make the legal move between rods and. If i % 3 = 1, make the legal move between rods and. In each iteration of this loop, we do something depending on what remainder we get when we divide by three. If is even then set the destination rod to the auxiliary rod and the auxiliary rod to the original destination rod.Compute the minimum number of moves needed to solve the puzzle, which is equal to (we will see later how we arrived at this number).Once again we have four inputs which are the same as in the recursive approach:

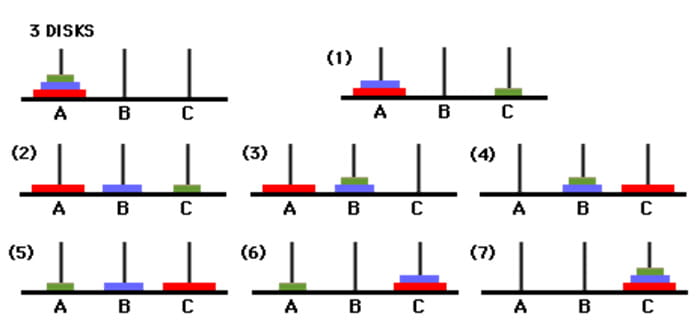
This approach is not as intuitive as the recursive method but it works nevertheless. The idea behind this method is to choose which pair of rods to make a legal move between, depending on what iteration of the algorithm we are on. Now let’s move the smallest disk to rod B as well:Īnother way to solve this problem is to think about it iteratively. So, it’s clear that we should move the second smallest disk. Moving the smallest disk will not accomplish much since moving it to rod A gets us back to the original state, and moving it to rod B is redundant since we could have just moved the smallest disk to rod B in the first place. Now we have two disks that we can move, namely the smallest and the second smallest.

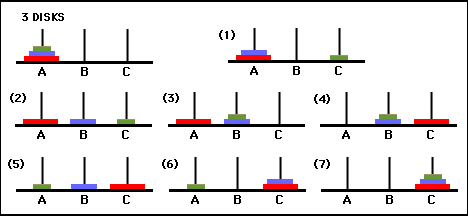
So let’s move the smallest disk to rod C: Our first move can only involve the smallest disk since there is only one stack and this disk is at the top of it. Let’s say the goal is to move all three disks to rod C (which rod we choose as our destination doesn’t matter). We start with all three disks stacked on one of the three rods (rod A in this case):

Let’s see an example of the puzzle in action when there are a total of three disks.

In each move, we must take the uppermost disk from one of the stacks and move it on top of another stack or to an empty rod.

A disk cannot be placed on top of another disk whose size is smaller.